机器学习笔记——02.模型的评估与选择

经验误差与过拟合

• 错误率：分类错误的样本数占样本总数的比例。m个样本中a个样本分类错误，则错误率E = a/m;
• 精度：1-错误率;
• 误差：学习器的实际预测输出与真实输出之间的差异；
• 训练误差/经验误差：再训练集上的误差
• 泛化误差：在新样本中的误差
• 过拟合：在训练集中拟合的很好，导致把一些样本的特性作为了“普遍规律”
• 欠拟合：与过拟合相反，并没有抓住普遍规律

评估方法

1. 留出法

   在数据集中找出一部分作为训练集，另一部分作为测试集。两部分互斥。一般两部分是2:1或4:1；

2. 交叉验证法

   一个数据集平均分成m个互斥的子集，每次取一个子集作为测试集，剩下的作为训练集，然后进行m次训练，每次训练测试集选择不同的子集。最后的评估结果按m次的均值计算；

3. 自助法

   随机选m次，每次选一个样本放入集合D’，将D-D’作为训练集。

4. 调参与最终模型

   • 调参：每个模型或算法都伴随着一些参数，而这些参数往往可能是一个范围，所以我们在这一个范围中根据一定的规律选择会更加方便快捷一点。

性能度量

​ 对学习器的泛化能力进行评估，不仅需要有效可行的实验估计方法，还需要有衡量模型泛化能力的评价标准，这就是性能度量。

• 错误率与精度

  • 错误率：是分类错误的样本数占样本总数的比例
  • 精度：分类正确的样本数占样本总数的比例

• 查准率、查全率与F1

  ​ 错误率和精度常用，但在某些任务中不能很好的满足需求，以搜索引擎调查为例：我们需要的用户体验结果数据是“在所有搜索推荐中有多少是用户需要的”或者“用户需要的有多少在搜索结果中”。为完成这样的结果，我们给出两个新的概念，“查准率”和“查全率”。

  ​ 在二分类问题，我们可以根据其真实类别与学习器预测类别的组合划分为“真正例”“假反例”“假正例”“真反例”

  

  • 查准率（P）：P = TP/(TP+FP)
  • 查全率（R）：R = TP/(TP+FN)

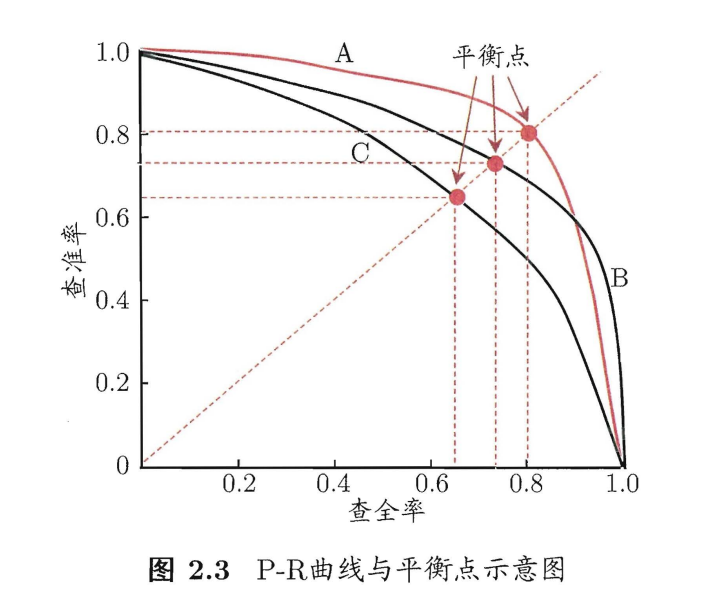
  查准率和查全率是两个相互矛盾的存在，查准率升高，查全率往往会下降；反之则相反。为了获得两项都不错的学习器模型，我们对预测结果的样例进行排序，排在前面的是学习器认为“最有可能”是正例的样本，后面的是“最不可能”是正例的样本。然后按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率。以查准率为纵轴，以查全率为横轴得到了”P-R曲线”。

  如何根据P-R曲线，判断学习器的好坏呢？

  1.如果一个学习器的曲线能完全包住另一个学习器的曲线，则第一个比第二个好。

  2.如果有交叉则可按面积大小。

  3.当然也可看“平衡点”（BEP），也就是P==R时的值。

  4.前三种太简化，我们会用F1度量（基于P和R的调和平均）。F1 = (2PR)/(P+R)=(2*TP)/(样例总数+TP-TN)

  5.Fβ，正注重对P与R的偏好问题。Fβ = [(1+β²)×P×R]/[(β²×P)+R];β=1退化为了标准的F1，β>1查全率重要，β<1查准率重要。

  6.宏查全率，宏查准率，宏F1。

  

• ROC与AUC

  ROC全称：“受试者工作特征”。纵轴是“真正例率”（TPR），横轴是“假正例率”（FPR）。

  TPR=TP/(TP+FN)

  FPR=FP/(TN+FP)

  如何根据ROC曲线，判断学习器的好坏呢？

  根据面积

  

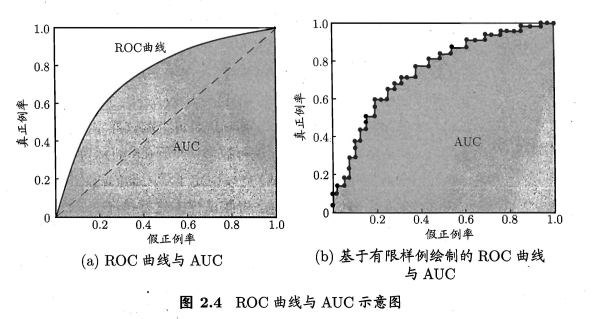
  AUC就是ROC各部分下面的面积

  AUC考虑的是学习器对样本预测的排序质量，误差与其有密切的联系。

• 代价敏感错误率与代价曲线

  在很多情况下，每次犯错所造成的结果是不一样的，也就导致犯错的代价也不同，例如：在医疗诊断中“把健康的人诊断成病人”和“把病人诊断成好人”前者是多做一次检查，后者则有生命危险。所以不同的错误应承担的风险不同，为了解决不同风险的问题，我们提出了“非均等代价”。

  以二分类任务为例，我们可以得到如下表格：

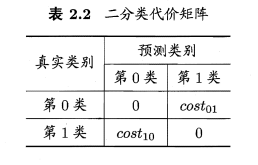
  其中cost i,j表示将第i类样本认做j类的代价。

  我们希望测得的代价是最小化的“总体代价”，那我们就不能只依靠“错误次数”还需要错误代价。也就有了“代价敏感”错误率：

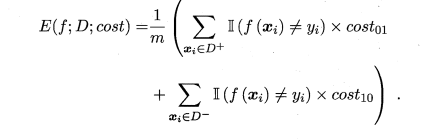
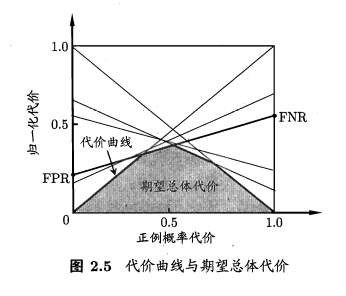
  在“非均等代价”的情况下，ROC曲线并不能很好的反应学习机的期望总体代价，所以我们选择了“代价曲线”：横轴是正例概率代价：P(+)cost = p×cost01/[p×cost01+(1 - p)×cost10]，其中p是正例的概率；纵坐标是归一化代价costnorm = [FNR × p × cost01 + FPR × (1 - p) × cost10]/[p × cost01 + (1 - p)×cost10]

  也可以写成：costnorm = FNR × P(+)cost + FPR × (1 - P(+)cost)；

  更深入理解：一条过A,B两点的直线方程可以写作y = µ × A + (1 - µ) × B，根据A,B的不同我们可以画出不同的直线，也就是说对于不同的FPR和FNR值我们能画出多条直线，这FPR和FNR值我们可以根据ROC曲线上的点来获取。

  而我们要的“期望总体代价”就是这些直线的下面的部分。

  如图：

比较检验

1. 假设检验

   ​

2. 交叉验证t检验

3. McNemar检验

4. Friedman检验与Nemenyi后续检验

偏差与方差

赏

谢谢你请我吃糖果

支付宝

微信